Downloads:
Introduction
This tutorial introduces key concepts used in the design of substation earthing and grounding systems. Important terminology is discussed including Grid Potential Rise, touch and step voltages and current distribution.
The behaviours of example earthing and grounding systems during a fault are explained.
Table of Contents
1 Grid Potential Rise (GPR)
Figure 1(a) shows a simple grounding system which consists of horizontal conductors (also called “mesh” or “grid” conductors) buried 0.5 m below the earth’s surface and 3 m long vertical conductors (also called “earth rods”) which are connected to the grid formed by the horizontal conductors. The horizontal grid is square and is subdivided into 4 square meshes.
Figure 1(b) shows the surface voltages which occur at the earth’s surface when the earthing system is energised during a fault.
When the electrical current is injected into the earth via an earthing system, the current is met by a resistance which depends directly upon the resistivity of the soil. Because of current flowing through this resistance, the electrical potential of the earthing system and all metallic structures connected to it rises. The maximum electrical potential that a substation earth grid may attain relative to a distant earthing point assumed to be at the potential of remote earth (0 Volts) is named Grid Potential Rise (GPR) [1].
The GPR is directly proportional to the magnitude of the current injected into the soil by the earthing system. For a given injection current, the GPR is directly proportional to the soil resistivity. Therefore, it is very important when designing an earthing system to have reliable soil resistivity measurements and to make them at the substation site in order to ascertain the soil properties. This is required to accurately model the earthing system performance.
For a given fault current, the GPR is approximately inversely proportional to the area of the grid. Note that the shape and burial depth of the grid also affect the GPR to some extent.
The GPR for the grid shown in Figure 1 is 2220 V and the maximum surface voltage, which is always lower than the GPR, is 2060 V.
Figure 1 – Example system and surface voltages plot
2 Touch and step voltages
Figure 1 shows the earth surface potentials are lower than the GPR and vary greatly. At points directly above a grid conductor, earth surface potentials are closest to the GPR; on the other hand, potential dips occur in the middle of grid meshes and the difference between the GPR and the earth surface potential is maximum at these centre points. This means that a person standing at the centre of a mesh and contacting any metallic structure which is connected to the earthing system, will be subjected to a high touch voltage.
Note that “touch voltage” is the difference in electrical potential between the earthing system and any earth surface location where a person can stand while contacting an energised metallic structure (assumed to be at the same potential as the earthing system) [1].
The plot in Figure 2 (a) displays touch voltages inside and up to 1 metre away from the grid. The maximum touch voltages typically occur at the corners of a grid because the highest leakage currents exist on the perimeter conductors (obtaining a leakage current plot is a way of showing this).
As Figure 1 and Figure 2 (b) shows, the steep potential gradient outside the earthing system perimeter could result in a significant potential difference appearing between two earth surface locations at which a person’s feet are positioned. It is generally assumed that a person’s stride will not exceed 1 m and a “step voltage” is therefore defined as the potential difference between two earth surface points 1 m apart.
Step voltage levels are usually much lower than touch voltages. Therefore, generally if safe touch voltages can be achieved for a design then step voltages should not be an issue.
Figure 2 – Touch and step voltages plots in two-dimensions
Touch and step voltages are, like GPR, directly proportional to the current injected into the earth. Furthermore, for a given injection current and a given set of grid proportions, touch and step voltages are directly proportional to the earth’s electrical resistivity.
In order to evaluate the performance of an earthing system, the GPR and the touch and step voltages occurring during fault conditions are compared with maximum acceptable values which are also known as maximum allowable or tolerable voltage limits. These safe limits are derived according to the IEC and IEEE Standard methods [1], [2].
Refer to the page that explains how to calculate touch and step voltage limits.
The safe limits are compared with the actual touch and step voltages for determining whether the design is safe. There are two main approaches to achieving a safe design:
- Reduce (or show) the actual touch and step voltages which appear at any point within the substation and around its perimeter are below the safe limits.
Increase the allowable limits by adding an additional surface layer of crushed rock or asphalt to the surface inside and outside the substation.
3 Fault current distribution
When an accidental energisation or “earth fault” occurs near a substation, large amounts of current flows from the faulted phase conductor and return to the power source through all conductive paths available (see Figure 3).
Figure 3 shows the flow of fault currents for two substations connected via an overhead transmission line if a fault occurs nearby to Substation A. The arrows indicate the direction of flow of the fault current. Here is a video tutorial explaining fault current distribution with worked examples.
During a fault a portion of the total fault current returns to the power (fault current) source along the following paths:
- Earth wires: a portion of the fault current flows from the fault site to the power source entirely via earth wires (if they exist). Another portion of the fault current flows along a length of the earth wires and is then injected into the earth by various earth paths such as transmission tower earths or earthing systems of substations other than the one nearest the fault.
- Substation earthing system: another portion of the fault current is injected into the earth by the earthing system of the substation near which the fault is occurring. From there, it flows through the earth to the earthing system of the power source, then through the earthing system of the power source, to the generator or transformer which is supplying the fault current.
- Auxiliary earthing system: if the substation has an earthing system in addition to the one at the substation site, then a portion of the fault current will be diverted into this additional earthing system. Note that the rebar in the reinforcing concrete floor of a building may be regarded as an auxiliary earthing system, as may a remote earth.
The portion of the fault current injected into substation earthing system is usually named Grid Current, which will cause potential rise in the earthing system.
The amount of fault current which will flow along each path depends directly upon their relative impedances. For example, if the earth wires provide a low impedance and do not span a great distance between the faulted substation and the power source, then they will tend to carry a greater proportion of the fault current than if they are long and of high impedance. Similarly, if the substation earthing system has a very low impedance, then it will conduct a much greater proportion of the fault current than if it has a high impedance.
In most cases the grid current is much less than the total fault current which is provided by the source. Therefore, it is worthwhile to analyse the fault current distribution during the design phase however additional information about the conductive paths is required.
4 Design to reduce GPR
An earthing system should be designed such that the GPR does not exceed 5000 V and this is mainly to protect equipment [3].
Reducing the GPR requires reducing the grid resistance and this is most effectively achieved by either increasing size of (area covered by) the grid or by adding rods which are driven into low resistivity bottom soil layers. The GPR can be reduced to a lesser degree by adding conductors to the interior of the grid.
Table 1 shows the calculated results from SafeGrid Earthing Software for four simple earthing systems. These earthing systems consist of a 20 m × 20 m square mesh buried 0.5 m deep, with rods (3 m length) added. Fault currents injected into the earthing systems and conductor cross-section areas are 1000 A and 70 mm2 respectively. A uniform soil model of resistivity 100 Ω.m is assumed.
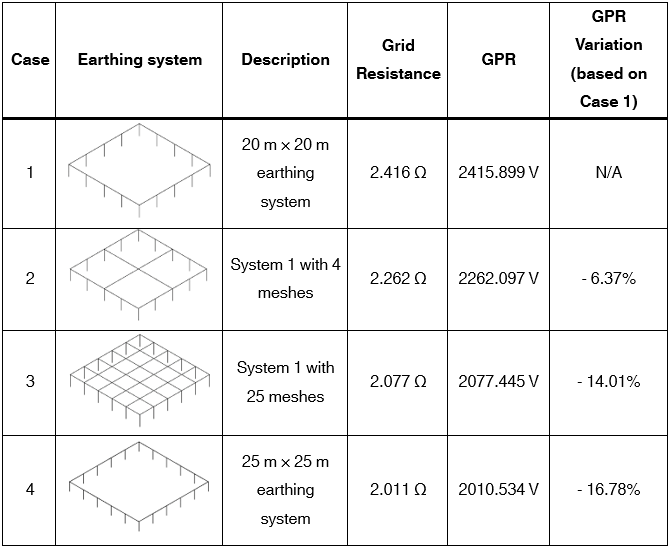
Starting with Case 1 and adding 2 additional 20 m long mesh conductors installed in the form of cross, the GPR decreases by 6.37 %. If 6 further 20 m long conductors are added to form the grid of Case 3 with a total of 25 meshes, the GPR decreases by 14.1 %.
Adding internal conductors to a grid is less effective than increasing its size. Case 4 shows that increasing the size alone from 20 m to 25 m, the GPR decreases by 16.78 %.
Note that reducing the grid resistance will increase the grid current resulting in a smaller reduction in GPR obtained assuming no current variation.
5 Design to reduce touch and step voltages
An earthing system must be designed so the touch voltages at any point within the substation perimeter, during a fault, are not dangerous. Because touch voltages are the difference in potential between a point on the earth’s surface and the substation earthing system, the ideal situation is for the potential of the earth’s surface to be close to the substation GPR.
The surface voltages and touch voltages plots for a 4 mesh grid are shown in Figure 4 (a) and (b) plots respectively. The 4 valleys in the surface voltages plot correspond to the centres of the 4 meshes and are the points at which the greatest touch potentials exist. The maximum touch voltage for this grid is 642 V.
Figure 4 – Surface and touch voltage plots for a 4-mesh grid
Figure 5 shows the surface voltages and touch voltages plots for the same grid but with 25 meshes. The increase in the number of meshes causes the valleys to become much shallower. The maximum touch voltages therefore become much smaller. The maximum touch voltage for this grid is 391 V.
Figure 5 – Surface and touch voltage plots for a 25-mesh grid
At some point, the improvement obtained by adding grid conductors becomes insignificant, in Figure 5, it is already apparent that not much improvement will be obtained by making the valleys shallower since the touch potential is already almost uniform throughout the grid area. In this case, if improvement is still required, the GPR itself must be lowered, for example, by increasing the size of the earthing system.
Step voltages within the substation area usually are not a problem if touch voltages are within safe limits. Not only are step voltages within the substation area smaller than touch voltages, but human beings also tolerate higher step voltages than touch voltages.
Step voltages are usually only a concern around the perimeter of the substation, where a steep earth surface potential gradient usually exists. As a rule of thumb, the steepness of the potential gradient is roughly inversely proportional to the size of the earthing system, step potentials are therefore liable to present a greater problem for small earthing systems than for larger ones. Increasing the size of the earthing system is an effective means of reducing step voltages.
Despite the touch voltages at the interior of the grid being reduced, the touch voltages on the edge of the substation are still very high. In order to protect personnel and equipment outside the substation, a buried grading ring (referred to as “perimeter conductors” in IEEE Std. 80) can be added 1 m beyond the main 20 m × 20 m earthing grid to reduce the touch voltages.
Figure 6 shows the touch and step voltages without grading ring. The maximum touch voltage is 767 V. Step voltages along the perimeter of the substation are also not acceptable.
Figure 6 – Touch and step voltages 2D plot without grading ring
Figure 7 shows the touch and step voltages with grading ring buried in a same depth as main grid. The installation of grading ring causes the touch and step voltages to reduce significantly. The maximum touch voltage decreases to 425 V and the step voltages along the perimeter of the substation are also reduced to around 50 V, compared with 200 V without grading ring.
Figure 7 Touch voltages 2D plot with grading ring
6 Effects of the soil resistivity structure on voltages
For an actual substation site, the soil resistivity structure is typically not uniform. For the majority of sites a multilayer soil model is more realistic and accurate for evaluating the earthing systems electrical performance.
In this section we examine the effects on surface voltages of the differences in the top and bottom layer resistivities for a simple two-layer soil. Most soil structures require a model of between 3 to 5 layers.
Typical two-layer soil models are:
- High-on-low model (top layer resistivity is higher than bottom layer resistivity)
- Low-on-high model (bottom layer resistivity is higher than top layer resistivity)
To demonstrate the different effects of high-on-low and low-on-high soils on the touch and step voltages, a simple 20 m × 20 m earthing grid without rods is used.
Figure 8 shows the surface voltages with high-on-low soil model of which the resistivity of top-layer soil is 500 Ω.m with depth of 1.5 m and bottom-layer soil resistivity is 50 Ω.m. The maximum surface voltage is 3595 V. For a high-on-low model the fault current which enters the top layer of high resistivity layer wants to escape into the bottom layer of low resistivity
Figure 8 – Surface voltages plots of high-on-low soil model
Figure 9 shows the surface voltages with low-on-high soil model of which the resistivity of top-layer soil is 50 Ω.m with depth of 1.5 m and bottom-layer soil resistivity is 500 Ω.m. The larger resistivity of bottom-layer soil impedes current flowing into the deep soil layers causing surface voltages to increase. The maximum surface voltage of low-on-high soil model reaches 5525 V.
Figure 9 – Surface voltages plots of low-on-high soil model
The bottom layer resistivity will have the most influence on the grid resistance and grid potential rise compared with the top layer (due to their relative thicknesses – the bottom layer thickness extends to infinite depth). Therefore, a low resistivity bottom layer will result in low overall grid resistance and GPR – this is the advantage. However, if the soil resistivity model is high-on-low then the touch voltages may be much greater than for low-on-high due to the steep variations in the surface voltages profile.
7 Using rods to improve safety
Ⅰ. Separate rods with consideration of the proximity effect
Rods installed in earthing system can improve performance, but rods need to be separated by adequate distance to be effective.
As Figure 10 shows, the field of a segment will influence adjacent segments and vice versa – reducing their ability to dissipate fault current, which is named proximity effect. Crowding multiple vertical rods is not as beneficial in terms of $/Ω as is achievable for fewer rods properly spaced.
A simple grid shown in Figure 11 with 4 of 5 m rods at each corner is built to illustrate this phenomenon. The rods are separated by 1, 2, 3, 4, 5, 7.5, 10 and 20 m. Grid (horizontal) conductors are insulated to ensure the results are only affected by spacing of rods.
Figure 12 shows the grid impedance with variation of the rods spacing. Note that the overall resistance is significantly reduced by separating up to the rods length. Therefore, it can be concluded that the rods need to be separated at a separation greater than one rod length.
Therefore, in general for rods to be effective they should be spaced by at least their length. For example, rods of 5 m length should be spaced by at least 5 m.
Ⅱ. Using rods effectively according to soil characteristics
The use of rods for reducing voltages can be less effective in some cases.
Table 2 shows the grid impedance of earthing systems with and without rods for different soil models. The installation of the rods reduces the grid impedance, especially for high-on-low soil model.
The grid impedance reduces by 86.14 % after adding the rods for high-on-low soil model, whereas use of rods on low-on-high soil model is not very effective (reducing by 24.53%) since currents are remaining in the topsoil layer. This problem can be resolved by installing counterpoise (horizontal conductors which extend outwards from the grid usually at the corners) for low-on-high soil model as it increases the are covered by the earthing grid. Increasing the area covered by the earthing grid will always improve performance.
References
[1] “IEEE Guide for Safety in AC Substation Earthing,” IEEE Std 80-2013.
[2] “Effects of current on human beings and livestock – General aspects.” IEC 60479-1:2018.
[3] “Maximum Limit of Allowable Ground Potential Rise of Substation Grounding System.” IEEE Transactions on Industrial Applications (Volume 51, Issue 6, 2015).