Table of Contents

Overview of the article
This technical paper presents and explains the results of professional design software for calculating emergency and cyclic ratings of high voltage (HV) electric power cables. The emergency and cyclic ratings are based on time-varying loading and are useful because they allow higher peak load currents than for steady-state (continuous) values. The calculations apply to situations where the properties of the time-varying load and the thermal properties of the cable system, including the thermal environment, are factored in.
I. Definitions of Emergency and Cyclic cable ratings
The definition of emergency rating is the permissible short-term rating of a cable already loaded and at a steady-state, considering the thermal capacitances and the thermal resistances of an installed cable system. The definition of cyclic rating is the maximum current of a cable when the load is varied in a sequence of steps that are repeated cyclically. The cyclic rating differs for different sequences and different cycle periods. Both emergency and cyclic ratings deal with time-varying loads.
The methods of calculating emergency and cyclic ratings of cables used in the software are based on the IEC Standards [1],[2]. These methods effectively deal with time varying loading by representing the physical cable system and its surroundings using a thermal ladder network of thermal resistances in series and capacitances in parallel where heat flow within the cable emanates radially to the outside of the cable and onto the environment. Fig.1 shows the thermal ladder network for a multicore HV cable.
The fundamental part of the calculations is to determine the transient temperature response of the cable. The transient temperature response is the response to a step of sustained rated load current. The transient calculations along with values from steady state rating calculations, are both used as inputs to the emergency and cyclic rating calculations.
According to the IEC Standard emergency ratings are applicable both for cables installed in air and buried cables (direct, in backfill and/or in ducts) whereas cyclic ratings only apply for buried cables.
II. Transient Response of a Cable
The complete transient temperature response θ_((t)) of a cable is given in Eq.1 where θ_(c(t)) is the partial temperature response of the cable itself, θ_(e(t)) is the cable environment temperature response and α_((t)) is an attainment factor.

To calculate the partial temperature response of the cable (including any ducts) one develops an equivalent thermal ladder network (refer to Fig. 1); a model for short and another for long duration transients. This ladder network is reduceable to a two-part thermal equivalent circuit consisting of lumped thermal resistances and thermal capacitances. The solution to the two-part network gives the partial temperature response of the cable.
The cable environment temperature response depends on the cable surroundings. For buried cables the important influencing factors are the soil thermal resistivity and the electrical losses resulting in mutual heating between adjacent cables. It is not necessary to calculate the cable environment temperature response for cables in air.
The attainment factor is calculated to account for the heat accumulation in the cable during the initial hours of the transient (refer to Section IV, E).
The complete transient temperature response is corrected for the variation in conductor losses with temperature and reduces conductor temperature overall (refer to Section IV, D).
Note responses for durations of transients less than 10 minutes are not recommended in the IEC Standards.
III. Emergency Ratings
The emergency rating of a cable is the current that can be applied to the cable without exceeding the maximum permissible temperature rise for a particular time duration (usually in hours). The emergency temperature limit is typically permitted to exceed the steady-state temperature limit for the cable.
The emergency rating calculations result in a scaling factor (greater than one) which is multiplied by the steady-state rated current. The IEC Standards state the calculated scaling factor shall not be greater than 2.5.
To calculate the scaling factor for a time-varying load cycle the load factor for the particular load cycle is required.
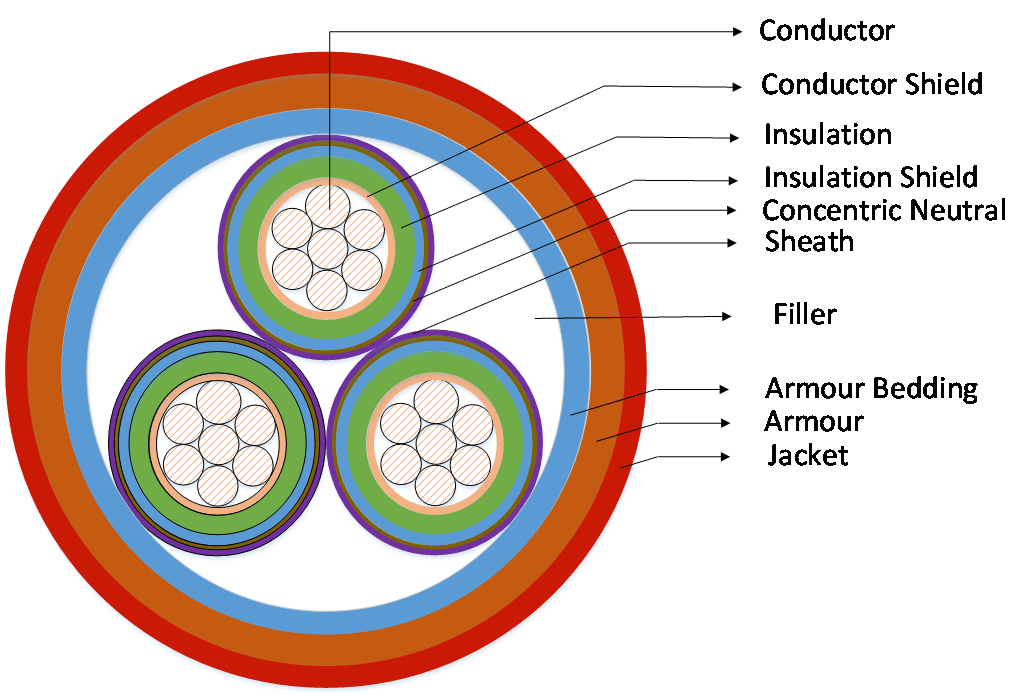
Fig. 1 – (a) Cable cross-section (b) Equivalent thermal ladder network comprising thermal resistances (T’s) and thermal capacitances (Q’s) of cable components
IV. Cyclic Ratings
The actual load on a cable will vary with time and often could be significantly less than the rated current; which gives rise to the cyclic rating. The cyclic rating depends on the shape of the daily load cycle.
The cyclic rating calculations result in a scaling factor (greater than one) which is multiplied by the steady-state rated current which gives the permissible peak value of the cyclic load current for the load cycle.
To calculate this scaling factor the loss-load factor and the stepped curve for the load cycle are required.
Calculation of load factor and loss-load factor
From a typical real-world load cycle, we calculate a load factor for the emergency rating calculations and loss-load factor for the cyclic rating calculations.
The user input is an hourly ratio of the cyclic load current to the maximum load current over a period of 24 hours. The average value of the load cycle current is the load factor. The loss-load factor is the average value of the square of the user input current (also used for plotting the stepped curve below).
Fig. 2 shows a load cycle and the generated step curve. The calculated daily load factor is 0.6544 and the loss-load factor, μ is 0.504.
V. Results
This section presents two case studies where emergency and cyclic ratings were calculated, one case study is for single core and another for a multicore HV cables. The results were calculated using Cable HV™ Software. The steady-state rating calculation results are presented as they are a prerequisite to the transient rating calculations.
Also, in this section there are three comparative studies which presents some important parameters and discusses their effects on the transient calculations.
The cable model data used for the case studies are given in Appendix. The load profile used was presented in Fig. 2. The times considered are up to 24 hours. The resolution of the calculations is to each second and the starting time of 10 minutes is governed by IEC 60853 [1].
A. CASE STUDY 1 - Single core cables
The first case study uses cable model 1, buried 1 m below the ground in a backfill with thermal resistivity 0.6 K.m/W as shown in Fig. 3. The cable is rated at 132 kV with a 1200mm2 single core copper conductor utilised in a three-phase system. The complete cable data is in the Appendix. The steady state current rating for this cable is 762 A. The thermal resistances for the cable is T1 = 0.43 K.m/W, T3 = 0.0937 K.m/W and T4 = 1.557 K.m/W. The conductor loss is 13.44 W/m and the total cable losses are 35.88 W/m.
Fig. 4 shows the transient temperature response for the cable with and without the conductor losses correction factor being applied (uncorrected is shown as a reference only as emergency rating always uses the corrected temperature values). The emergency rating is shown as a function of time and reduces with increasing temperature
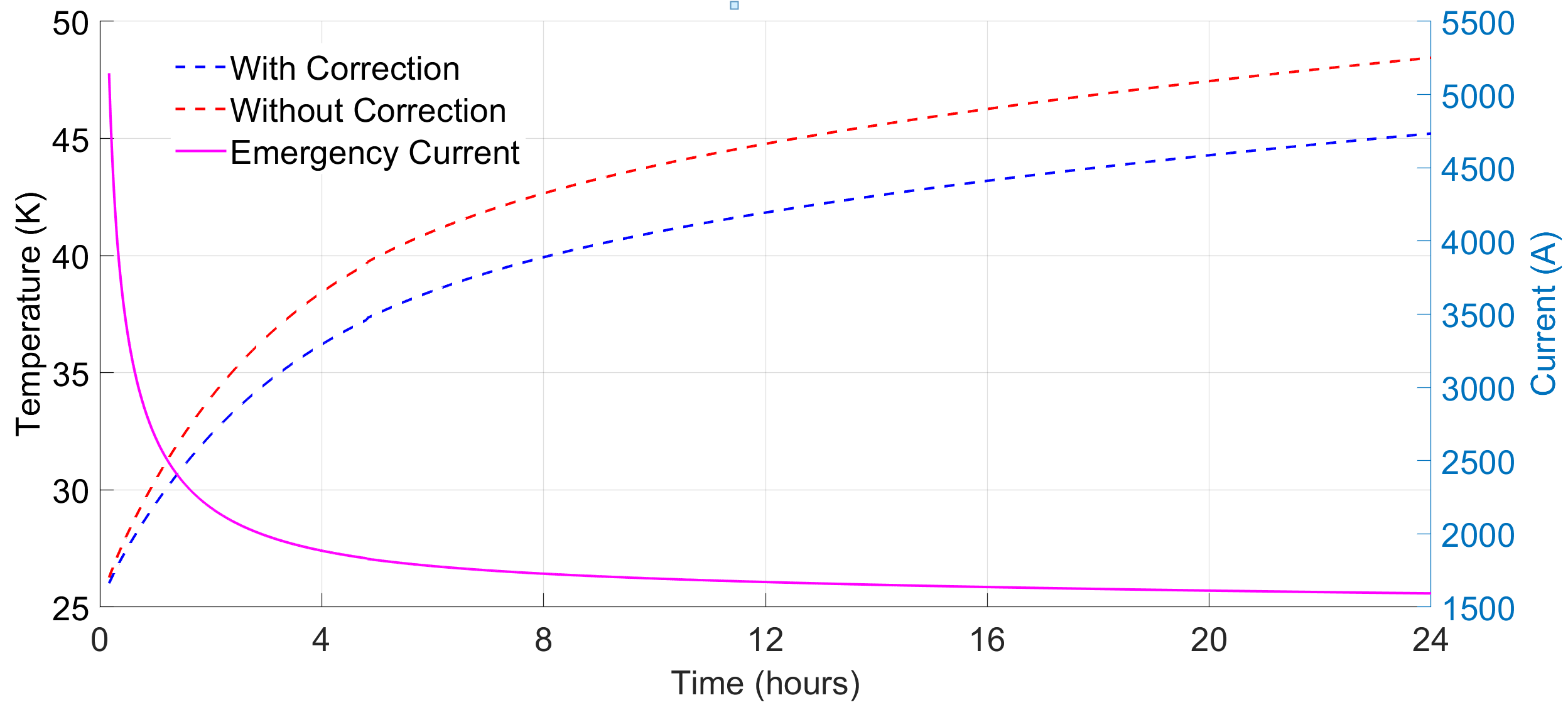
Table I also shows the emergency rating of the cable is significantly greater than the steady-state rating.
| Emergency time (hours) | Rating (A) |
|---|---|
| 1 | 2662 |
| 2 | 2179 |
| 4 | 1885 |
| 8 | 1728 |
| 12 | 1671 |
| 24 | 1594 |
| Steady-state | 762 |
The cyclic rating factor was calculated to be 1.33143. Hence since the steady-state rating is 762 A then the permissible peak of the cyclic load current for a 24-hour period is 1015 A.
B. CASE STUDY 2 - Multi-core cables
The second case study considers two multicore cables, cable model 3 and cable model 4, buried at 1 m below the ground and separated by 0.5 m as shown in Fig. 5. The cable data are given in Appendix. The steady state current rating for cable model 3 (500 mm2 conductors) is 523 A and that of cable model 4 (240 mm2 conductors) is 367 A including a reduction in both ratings caused by the mutual heating between cables.
The thermal resistances for cable model 3 are T1 = 0.240 K.m/W, T2 = 0.149 K.m/W, T3 = 0.067 K.m/W and T4 = 1.168 K.m/W. The conductor loss for cable model 3 is 14.02 W/m and the total cable losses are 42.93 W/m.
The thermal resistances for cable model 4 are T1 = 0.312 K.m/W, T2 = 0.161 K.m/W, T3 = 0.7 K.m/W and T4 = 1.26 K.m/W. The conductor losses for this cable model is 13.25 W/m and the total cable losses are 40.13 W/m.
Fig. 6 and Fig. 7 shows the transient temperature response of two circuits (including mutual heating), each consisting of one multi-core cable when the conductor losses correction factor has been applied. The emergency rating is shown as a function of time which reduces with increasing temperature
The emergency ratings are given in Table II.
| Emergency time (hours) | Rating (A) | Rating (A) |
|---|---|---|
| Cable model 3 | Cable model 4 | |
| 1 | 1413 | 918 |
| 2 | 1275 | 848 |
| 4 | 1177 | 795 |
| 8 | 1106 | 756 |
| 12 | 1073 | 738 |
| 24 | 1025 | 709 |
| Steady-state | 523 | 367 |
The cyclic ratings were not calculated since the IEC supports multiple equally loaded circuits (same cable types) and does not support multiple circuits with different losses.
C. Variation of emergency ratings with and without backfill
The emergency ratings of a cable depend on the transient conductor temperature plus the initial steady state current. Fig. 8 below shows two separate laying conditions for cable model 5; one being in native soil another in backfill. The height of the backfill is 0.5 m and its width is 1 m. The thermal resistivity of the backfill is 0.6 K.m/W and that of the native soil is 1.5 K.m/W. The steady state rating for directly in native soil is 746 A and that in backfill is 889 A.
The steady state results for the cable in both installations are: T1 = 0.388 K.m/W, T3 = 0.092 K.m/W
Without backfill, T4 = 1.867 K.m/W. The conductor loss is 10.587 W/m and the total cable loss is 31.07 W/m.
With backfill, T4 = 1.244 K.m/W. The conductor losses for cable model 1 is 15.03 W/m and the total cable losses are 44.25 W/m.
Fig. 9 compares the emergency ratings for both with and without backfill. The plots show that the emergency ratings are higher for the cable in backfill case since the thermal resistivity of the backfill is lower than that of the native soil. Initially the emergency ratings for both cases are similar, but as emergency time is increased the ratings vary to a greater degree. This time-dependent variation is due to the effects of the backfill on emergency ratings also being incorporated into the transient calculations.
The emergency ratings are given in Table III.
| Emergency time (hours) | |||
|---|---|---|---|
| Rating (A) | |||
| In Native Soil | With Backfill | Rating (A) | |
| 1 | 969 | 959 | |
| 2 | 881 | 815 | |
| 4 | 820 | 742 | |
| 8 | 776 | 707 | |
| 12 | 756 | 693 | |
| 24 | 729 | 693 | |
| Steady-state | 554 | 596 | |
D. Correction for variation of conductor losses with temperature
During the operation of a cable the conductor temperature is regularly changing with time and conductor losses are variable. Consider cable model 2, (400 mm2, 11 kV) directly buried 1 m below the ground as shown in Fig. 10 carrying steady-state rated current (load factor is unity) of 522 A.
The steady state results for the cable is: T1 = 0.197 K.m/W, T2 = 0.16, T3 = 0.069 K.m/W and T4 = 1.891 K.m/W. The conductor loss is 17.47 W/m and the total cable losses are 53.31 W/m
Fig. 11 compares the transient temperature of the cable and Fig. 12 compares the emergency currents over 24 hours with and without applying the correction factor
The emergency ratings and the transient temperature response of the cable with and without the correction factor are shown in Table IV.
| Emergency time (hours) | Transient Temperature (K) | Rating (A) | ||
|---|---|---|---|---|
| With Correction | Without Correction | With Correction | Without Correction | |
| 1 | 33.5 | 35.3 | 831 | 784 |
| 2 | 36.5 | 38.8 | 759 | 724 |
| 4 | 40 | 42.7 | 709 | 682 |
| 8 | 43.8 | 46.9 | 673 | 652 |
| 12 | 46.1 | 49.4 | 657 | 639 |
| 24 | 50.2 | 729 | 635 | 621 |
E. Variation of attainment factor with and without ducts
The attainment factor (a factor ≤ 1) is the correction (reduction in temperature) that is applied to the environmental partial temperature response of the cable to compensate for the initial temperature absorption by the cable components including any ducts (refer to Eq.1).
This section examines the variation of the attainment factor cable model 3 installed as directly buried and when in ducts as shown in Fig. 13. The duct outer diameter is 0.125 m.
The steady state thermal resistances are T1 = 0.24 K.m/W, T2 = 0.150 K.m/W and T3 = 0.067 K.m/W for both cases.
When the cable is directly buried the steady-state rating of the cable is 596 A and T4 = 0.852 K.m/W. The conductor loss is 17.9 W/m and the total cable losses is 54.81 W/m
When the cable is installed in ducts the steady-state rating of the cable is 554 A and T4 = 1.035 K.m/W. The conductor loss is 15.42 W/m and the total cable losses are 47.22 W/m.
Fig. 14 shows the attainment factor for the directly buried case reaches unity after 2 hours while that of the cable in ducts case reaches unity after a much longer time of 12 hours.
Fig. 15 shows that the initial temperature for the direct buried case is higher than for the case in ducts due to the initial higher (being nearer to unity) attainment factor.
The emergency ratings are shown in Table V.
| Emergency time (hours) | Transient Temperature (K) | |
|---|---|---|
| Direct Buried | In Ducts | |
| 1 | 969 | 959 |
| 2 | 881 | 815 |
| 4 | 820 | 742 |
| 8 | 776 | 707 |
| 12 | 756 | 693 |
| 24 | 729 | 693 |
| Steady-state | 554 | 596 |
VI. Conclusions
VII. Appendix – Cable Parameters
| Cable Parameters | Cable Model 1 | Cable Model 2 | Cable Model 3 | Cable Model 4 | Cable Model 5 |
|---|---|---|---|---|---|
| Cable Data | |||||
| Voltage (kV) | 132 | 11 | 22 | 22 | 132 |
| Cores | Single | Multi | Multi | Multi | Single |
| Conductor Area (mm²) | 1200 | 400 | 500 | 240 | 1600 |
| Conductor Diameter (mm) | 43 | 23.6 | 26.5 | 18.5 | 49.8 |
| Conductor Screen Diameter (mm) | 49 | 25 | 28 | 19.8 | 55.8 |
| Conductor Screen Thickness (mm) | 3 | 0.7 | 0.75 | 0.65 | 3 |
| Insulation Diameter (mm) | 89 | 31.8 | 39 | 30.8 | 95.8 |
| Insulation Thickness | 20 | 3.4 | 5.5 | 5.5 | 20 |
| Insulation Screen Diameter (mm) | 93.2 | 33.6 | 40.8 | 32.4 | 100 |
| Insulation Screen Thickness (mm) | 2.1 | 0.9 | 0.9 | 0.8 | 2.1 |
| Sheath Diameter (mm) | 98.2 | - | - | - | 105 |
| Sheath Thickness (mm) | 2.5 | - | - | - | 2.5 |
| Concentric neutral Diameter (mm) | 99.9 | 35.3 | 42.5 | 34.1 | 106.7 |
| Concentric neutral Thickness (mm) | 0.85 | 0.85 | 0.85 | 0.85 | 0.85 |
| Armour bedding Diameter (mm) | - | 81.2 | 97.1 | 78.5 | - |
| Armour bedding Thickness (mm) | - | 2.56 | 2.76 | 2.51 | - |
| Armour Diameter (mm) | - | 87.5 | 103.4 | 84.8 | - |
| Armour Thickness (mm) | - | 3.15 | 3.15 | 3.15 | - |
| Jacket Diameter (mm) | 110.2 | 95.5 | 112.5 | 92.6 | 117.5 |
| Jacket Thickness (mm) | 5.15 | 4 | 4.55 | 3.9 | 5.4 |
References
- “IEC Standard 60853-1”, Calculation of the Cyclic and Emergency Current Ratings of Cables. Part 1: Cyclic Rating Factor of Cables up to and including 18/30 (36) kV 1985.
- “IEC Standard 60853-2”, Calculation of the Cyclic and Emergency Current Ratings of Cables. Part 2: Cyclic Rating Factor of Cables Greater than 18/30 (36) kV and Emergency Ratings for Cables of All Voltages, 1989
- Cable HV Software Version 3.7: https://elek.com/electrical-software/elek-cable-high-voltage/