What is cable charging current?
Charging current is defined as the current that flows through the shunt capacitance of a transmission line and is present in both underground cables and overhead lines. The shunt capacitance and hence the charging currents for underground cables are 10-20 times larger than for overhead lines. Note that for overhead lines, the series inductance is 2-3 times larger than underground cables [1].
Charging current increases linearly with the cable length also increases with voltage level and becomes an important consideration for long cable transmission; usually 40 km or longer transmission voltages lower than 220 kV and 20 km or longer for transmission voltages 220 kV or above [2].
The effect of charging current is that to supply the active load, the current injected at the source needs to be higher to compensate for the cable capacitance. Charging current generates heat losses in the cable that can be as high as the thermal rating of the cable for long transmission lines.
Note that the phenomena of charging current and the limitation it imposes on maximum transmission line length is applicable for AC cables only. In contrast to AC cables, the absence of charging current in DC cables leads to virtually unlimited transmission distances via DC.
Charging current equations
The equation for charging current (for AC cables) can be expressed as:

- C = capacitance per unit length (μF/km)
- ω = angular frequency of voltage (s-1)
- U = RMS line voltage (phase to phase) (kV)
- L = Length (km)
- IC = Charging current (A)

- ε = relative permittivity of the insulation ( = 2.5 using XLPE)
- Di = external diameter of the insulation (excluding screen) (mm)
- dC = diameter of conductor including screen, if any (mm)
Critical length of cables
As the cable length increases, the current delivered to the load decreases because of increasing charging current. The length at which the charging current becomes equal to the supply current is defined as the critical length and it is at this point the charging current accounts for all heat losses in the cable. The equation for critical length is:

- LC = Critical length (km)
- IS = Rated supply current from source or sending end (A)
- U = RMS line voltage (phase to phase) (kV)
Calculating active power received by the load
The maximum transmitted power received at the load point for an underground radial link is dependent on the supply frequency and voltage, the cable length, the voltage across the insulation and cable capacitance [1]. To calculate the total active power received at the load based on the length of the transmission line, the following equation can be used:

Where:
- PL = Active power (at ) at the load point
- SG = Feeding power at the source (MVA)
- L = Length of underground link (km)
Apparent power SG at the source can be calculated as follows assuming a 3-phase configuration:

Where:
- PL = Active power (at ) at the load point
- SG = Feeding power at the source (MVA)
- L = Length of underground link (km)
Apparent power SG at the source can be calculated as follows assuming a 3-phase configuration:
Compensation of charging current
To compensate for cable capacitive reactance, shunt inductive reactors are inserted. This is normally needed for long cable routes. A rule-of-thumb would be to consider compensation if the transferable active power has decreased by roughly 15% [3].
The ratings of reactors must consider the cable systems ability to cope with voltage dips for no-load conditions as well as provide compensation of the charging current for full-load conditions. Shunt reactors can be placed at regular intervals, but this arrangement may prove to be costly and hence a thorough system analysis is needed for optimal performance. A simple formula can be applied which summarises the reactive power requirements of underground cables [1]. It should be noted that these equations provide only a basic indication for cable compensation and should be used for a preliminary power system study.
An approximation for the inductance value can be deduced using a simple formula as shown below:

- Most likely going to remove equations (6) and (7) as said in the email.
Where
- Lshunt= Shunt inductor (H)
- Qcable = Cable reactive power (VAR)
- CT = Total cable capacitance over entire transmission length (F)
Examining critical length
Example 1 – 132 kV and 22 kV cables both carrying 531 A
Figure 1 displays a comparison test with a 132 kV cable against a 22 kV cable. Each cable supplies 20.23 MW at a voltage of 22 kV and carries a current of 531 A. By using a higher rated voltage cable, the critical length extends further due to lower capacitance ratings. The lower capacitance rating is due to the increase in insulation thickness of the cables and can be calculated from (2).
As can be seen from figure 1, when both cables are supplying the same active power, the 132 kV cable extends further to 928 km compared to the 22 kV cable at only 386 km. At the 386 km mark, the active power for the 132 kV cable is 18.4 MW. This represents only a 9% decrease from the nominal supply rating and therefore, a higher voltage rated cable could be used to improve power efficiency for the designer’s intended transmission length.
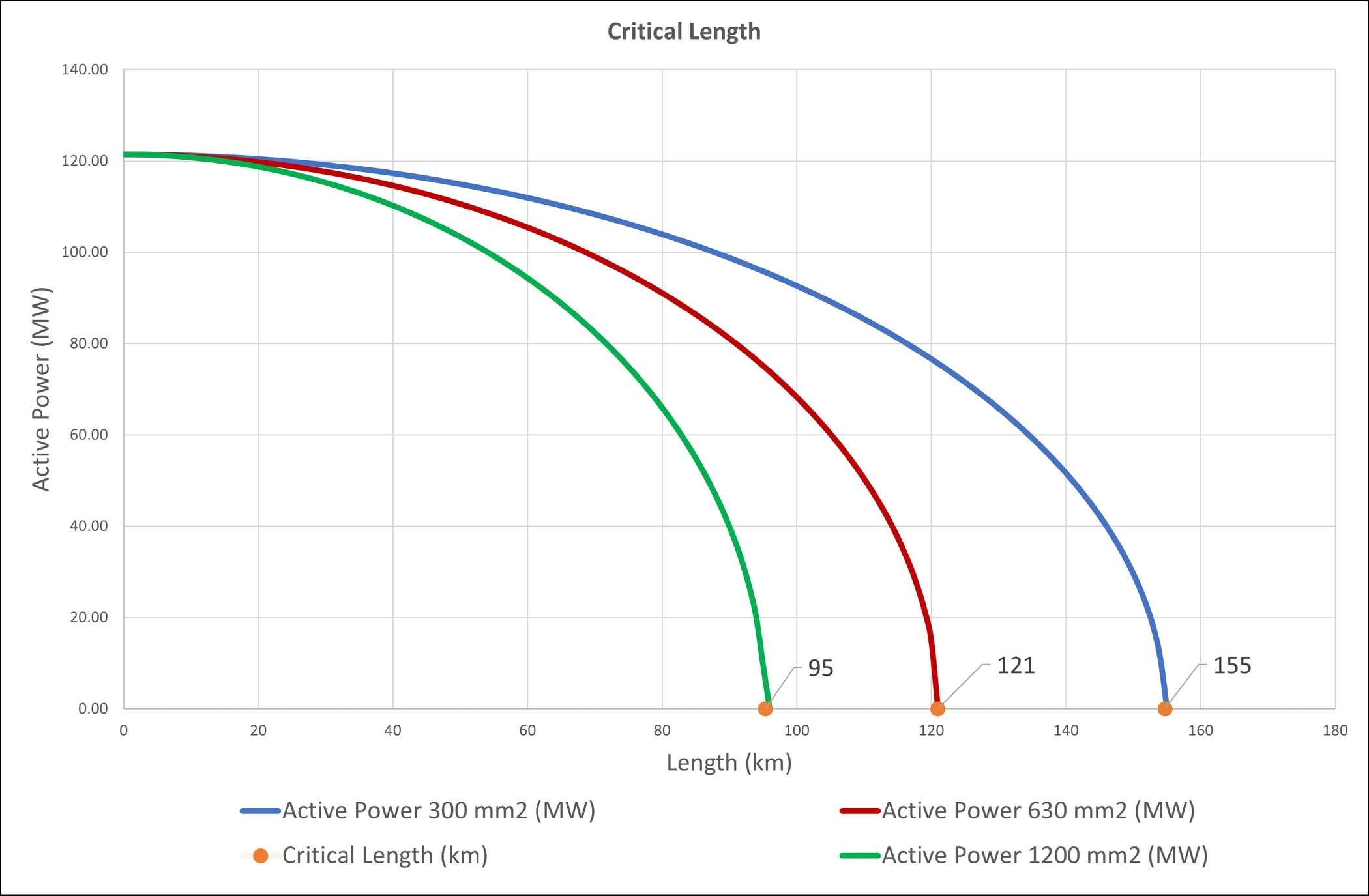
Example 2 – Single core 132 kV cables of different sizes
Figure 2 shows a comparison test using a single core 132 kV cable of three different sizes – 300 mm2, 630 mm2 and 1200 mm2. Each of the different cross-sectional cables supply 121.4 MW of power with a voltage of 132 kV and a current of 531 A. The cables in each circuit are touching, arranged in trefoil and are buried 0.5 m below the ground. As the conductor diameter increases, the critical length decreases. Although the insulation thickness remains the same for all the cables, the capacitance increases due to the increase in conductor size.
Example 3 – Buried 132 kV cables at 50 Hz and 60 Hz
Figure 3 displays two plots with different system frequencies whereby both circuits are rated at 132 kV, buried at 0.5 m, are touching and trefoil arranged with a cross-sectional area of 300mm2. The 60 Hz (green) plot has a shorter critical length than the 50 Hz (blue) plot. As frequency increases, critical length decreases as a result and can be seen from (3).
References:
- CIGRE, “General Guidelines for the Integration of a New Underground Cable System in the Network – Working Group B1.19”, CIGRE, 2004. Accessed on: Sep., 12, 2020. [Online]. Available: https://e-cigre.org/publication/250-technical-and-environmental-issues-regarding-the-integration-of-a-new-hv-underground-cable-system-in-the-network
- CIGRE, “Implementation of Long AC HV and EHV Cable Systems – Working Group B1.47”, CIGRE, 2017. Accessed on: Sep., 14, 2020. [Online]. Available: https://e-cigre.org/publication/680-implementation-of-long-ac-hv-and-ehv-cable-systems
- CIGRE, “A Guide for Rating Calculations of Insulated Cables – Working Group B1.35”, CIGRE, 2015. Accessed on: Sep., 12, 2020. [Online]. Available https://e-cigre.org/publication/640-a-guide-for-rating-calculations-of-insulated-cables
- Electric Cables – Calculation of the Current Rating – Part 1-1: Current Rating Equations (100% load factor) and calculation of losses – General, IEC 60287-1-1:2014
- Cable High Voltage Software Version 4.3 (2021). Electrotechnik.
Try our High Voltage Cable Ratings Calculations Software to IEC 60287 for free.